
如何求函数的值域?
1,分离常数法。
求函数的值域方法很多,其中第一种方法就是常见的分离常数法,这在基本不等式当中已经学过分离常数的技巧,简单的说就是配凑法。

分离常数法

分离常数法
2,分离常数法或判别式法。
下面这道题很典型,可以用常规的分离常数法,变成求复合函数的值域。但最简单的方法是根的判别式法,通过整理成一个一元二次方程,利用根的判别式列不等式,非常的快捷方便。但要特别讨论二次项系数,这一点往往容易被忽略。

根的判别式法
3,换元法
在高中数学中,换元法是一种运用非常广泛的方法。在使用这个方法的过程当中,一定要特别注意元的取值范围,如果忽略了这一点,求出函数的值域就是不准确的。
给大家列举了三道经典的换元法,第一款是带根式的,换元成二次函数。第二款是带指数函数的,特别注意取值范围。第三款是对数函数,转化成复合函数求值域。
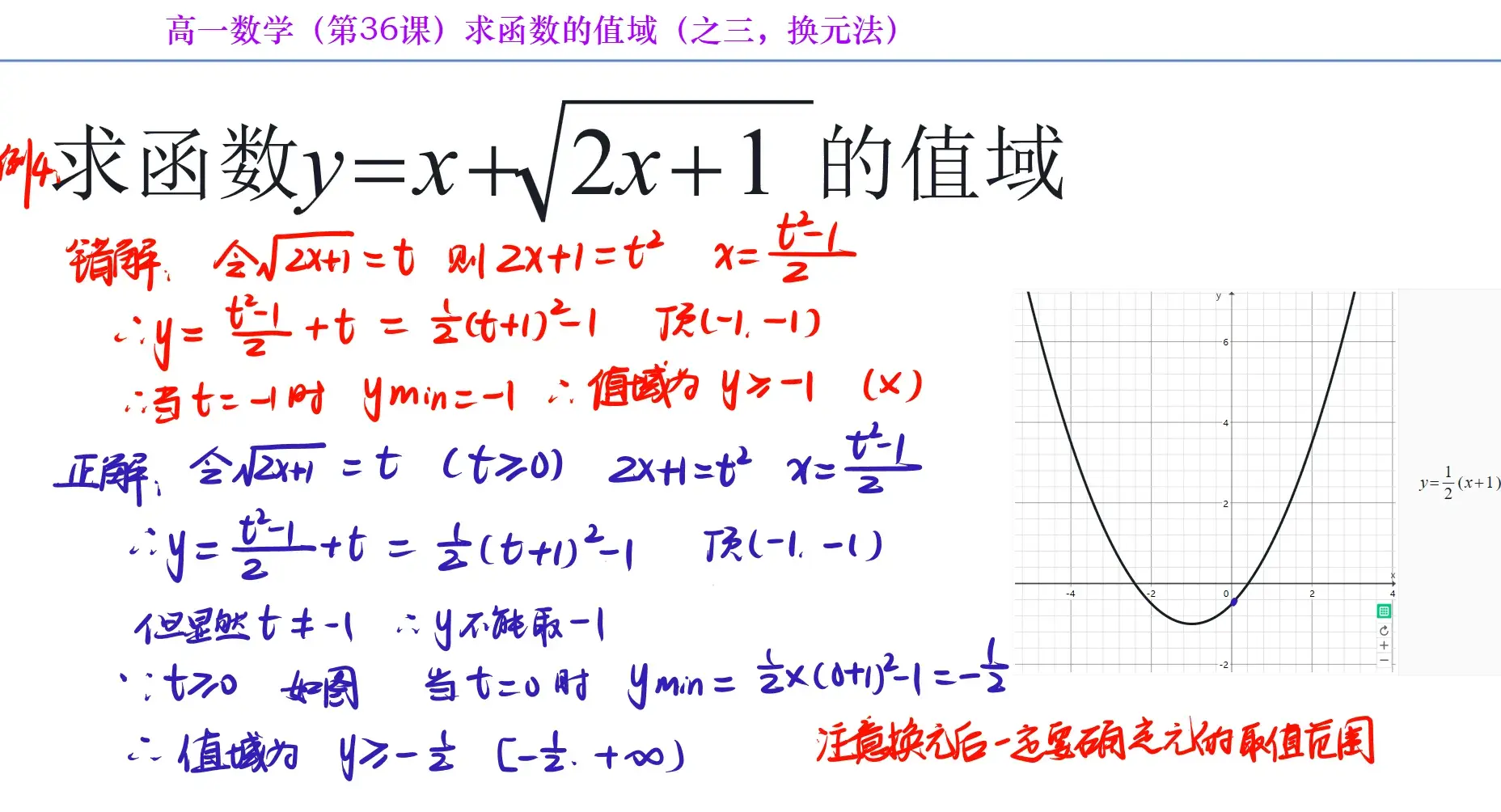
换元法之一。

换元法之二

换元法之三。
4,三角换元法
这个内容要用到最后一张三角函数,大家先掌握什么款式的题目可以用三角换元法,在设三角函数的时候,要特别注意角的取值范围。

三角换元法
像上面这种款式的题目通常可以用三角换元法,主要武器就是同角的正余弦的平方和等于1,所以可以通过开方把根式去掉。我已经把题目的细节写在上面,但是要注意易错点。不清楚的可以看看我发的视频,这篇文章的每一道题我都发了解题视频。

三角换元法

三角换元法
其实这上面的每一道题可能都有很多种方法,你掌握的方法越多,数学思维就越容易拓展。




